아주 기본적인 통계 용어를 알아보겠다.
평균: 일반적으로 산술평균을 의미. 총 n개의 데이터가 있을 때, 산술 평균 A는 다음과 같다.
- A = (a1 + a2 +... an) / n
- 데이터의 분포가 대칭적인 경우 효과적. ex) 정규분포
중앙값: 주어진 값들을 크기 순으로 정렬했을 때, 가장 중앙에 위치하는 값.
- 데이터의 분포가 한쪽으로 치우쳤을 때, 이상치(outlier)가 존재할 때 효과적.
기댓값: 각 사건에 대해 확률 변수와 확률 값을 곱한 것을 모두 더한 값. 산술 평균과 유사.
- E[X] = ∑i {(i 번째 사건이 발생할 확률) * (i 번째 사건에 대한 확률 변수)} = ∑i {P(Xi) * Xi}
- X가 연속확률 변수라면, 확률분포 함수 f를 이용해서 E[X]를 계산 가능.
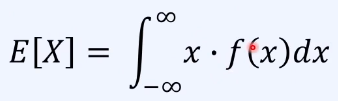
- 평균과 기댓값은 유사하지만, 사용되는 상황이 다름.
- 기댓값: 새로운 데이터가 관측되었을 때, 그 데이터가 확률적으로 어떤 값을 가질지를 예측할 때 이용.
- 평균: 이미 주어진 값에 대해 통계적인 특성을 분석할 때 이용.
- 예: 1000원짜리 복권이 있을 때, 기대 이익(수익-비용)은?
- 1/10 * (5000 - 1000) + 1/10 * (1000 - 1000) + 6/10 * (0 - 1000) = -200

분산: 데이터가 얼마나 흩어져있는지를 나타내는 척도.
- 평균과 관측치에 대한 편차의 제곱의 평균.
- 편차: 관측값 - 평균
- 편차는 평균과의 차이이기 때문에, 편차들의 전체 합은 0 → 편차의 제곱의 합을 계산하기.
- N개의 데이터의 평균이 µ 일 때 분산은 아래와 같다.
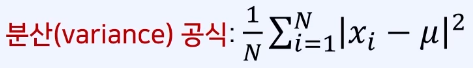
- 분산이 작다: 각 데이터가 평균에 근접한다는 의미.
- 분산이 크다: 각 데이터가 평균에 멀리 있다는 의미.

표준편차: 분산의 양의 제곱근.
- 분산은 편차의 제곱이기 때문에 값이 너무 큰 경향이 있음 → 분산에 양의 제곱근을 하여 표준화하기.

지금까지 아주 기본적인 통계 개념을 알아보았고,
다음 시간에는 확률 변수가 여러 개일 때 분산을
어떻게 계산할 수 있는지 알아보겠다!
'Part1. 딥러닝 시작 전 > Chapter 1. 통계' 카테고리의 다른 글
| 7. 최대 가능도 추정 (0) | 2023.07.06 |
|---|---|
| 6. 공분산과 상관계수 (0) | 2023.07.05 |
| 4. 조건부 확률과 베이즈 정리 (0) | 2023.07.04 |
| 3. 결합 확률과 주변 확률 (0) | 2023.07.03 |
| 2. 확률 분포의 종류와 활용 (0) | 2023.06.30 |



