선형 회귀(Linear Regression)
- 주어진 데이터를 학습하여 가장 합리적인 선형 함수를 찾아내는 문제.
- 하나의 스칼라(실수)를 예측할 수 있다.
- 가설 함수(선형 함수 모델): f(x) = Wx + b
- 선형 회귀에서 학습: 모델(W, b)을 수정하면서 가장 합리적인 식을 찾는 것.
- 비용(손실, loss)을 최소화 작은 모델이 합리적인 모델.
- x는 scalar 혹은 벡터가 가능함.
- 선형 회귀에서 학습: 모델(W, b)을 수정하면서 가장 합리적인 식을 찾는 것.

최소제곱법(Least Square Method)
- 평균제곱오차(MSE)를 이용해 비용을 최소화하는 방법이다.
- m개의 데이터가 있을 때 cost는 아래와 같고, cost를 최소화하는 W, b를 찾는 것이 목표.
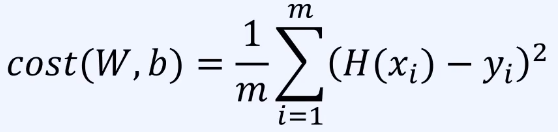
경사하강법
- 최소제곱을 얻는 방법 중 하나.
- Cost 함수를 W로 미분(기울기)했을 때 절댓값이 최소 → cost가 가장 최소.
- 모델을 학습시킨다 = W를 기울기의 반대 방향으로 업데이트한다.
- 기울기가 +이면 W를 왼쪽으로 이동, -이면 W를 오른쪽으로 이동.
- 학습률(learning rate: 한 번에 W를 얼마나 이동시킬 것인지)에 따라 학습 속도가 다르다.
- 학습 과정을 반복하면 가중치 W는 올바른 지점으로 수렴함.
- 모델을 학습시킨다 = W를 기울기의 반대 방향으로 업데이트한다.

이것으로 딥러닝을 위한 통계 이론은 끝이다!
다음시간에는 딥러닝을 위한 자료구조를 알아보겠다.
'Part1. 딥러닝 시작 전 > Chapter 1. 통계' 카테고리의 다른 글
| 8. 편향과 오차 (0) | 2023.07.06 |
|---|---|
| 7. 최대 가능도 추정 (0) | 2023.07.06 |
| 6. 공분산과 상관계수 (0) | 2023.07.05 |
| 5. 평균/기댓값/분산/표준편차 (0) | 2023.07.05 |
| 4. 조건부 확률과 베이즈 정리 (0) | 2023.07.04 |



